Reflections on Projections (and vice-versa)

This morning the esteemed Dr. Kenneth Field (is this an honorary title? How much do we really know about Ken?) tweeted a note about his wonderful book, Cartography. I am easily distracted by shiny things so my attention was immediately drawn to the ornament festooning the magnificent tree in Ken’s post.

Pondering

I like to peer into reflective surfaces in images to see if I can get a sense of the studio or the photographer. This is a thing people do.

Then I publicly wondered if I could georeference the globe over an orthographic projection and then unwrap it, to un-spherically-distort the reflection and peer into Ken’s living room (a longstanding dream of mine). So I asked Twitter for someone to send me a picture of themselves reflected in a shiny Christmas ornament. Christopher Pollard sent me one right away.

Georeferencing

Maybe three minutes later Christopher was peeled off of his reflective sphere into an equirectangular surface.

Ah the simple joys of inappropriate uses of georeferencing.

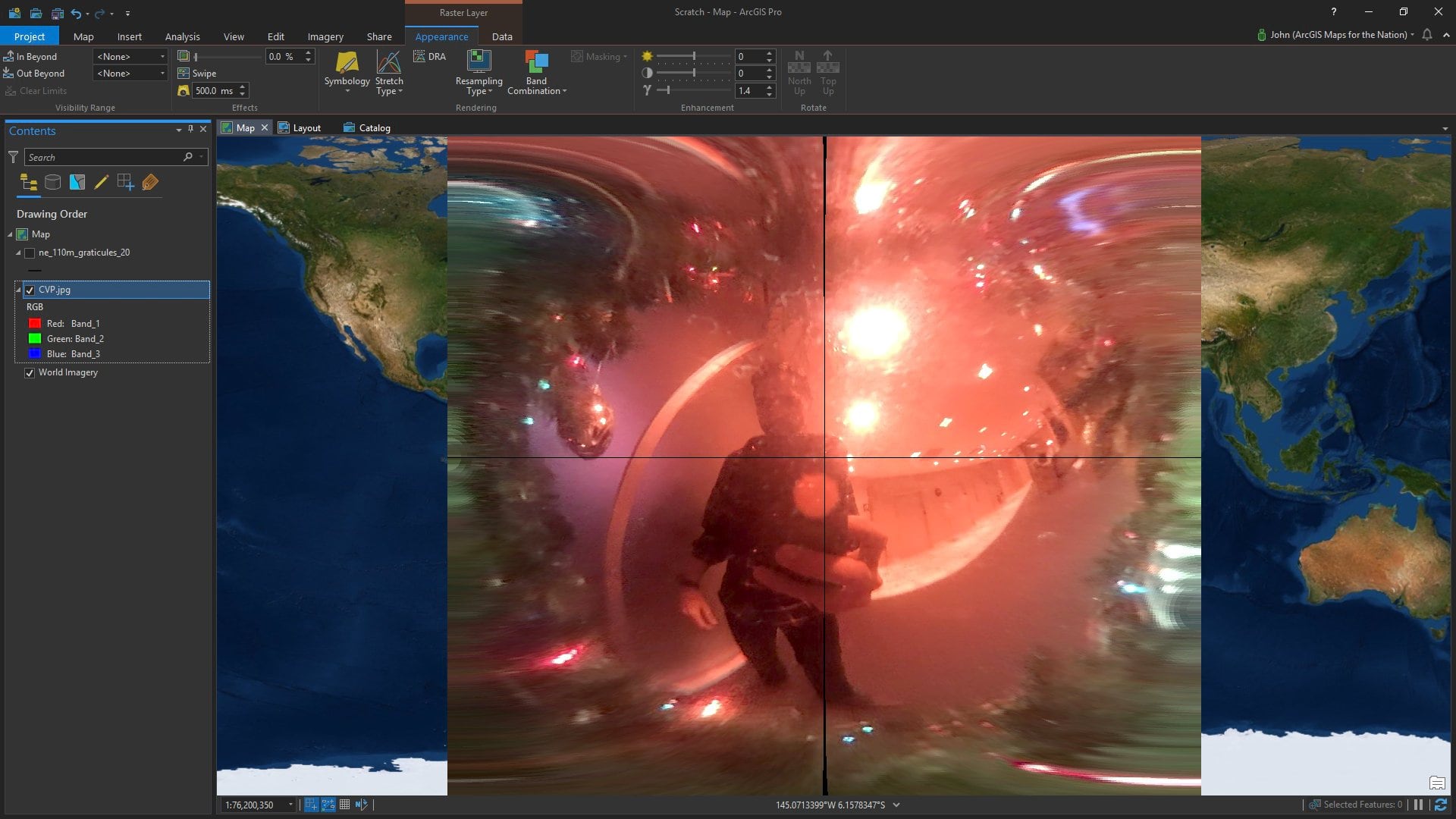
I tried it out on a couple spheres I have in the office. Here’s me (and my office-mate Pepper the collie) reflected on a Baoding ball.

You might notice a faint cyan graticule. I added that to make the georeferencing easier.

Since this is already a sphere, I set the projection to the World From Space (an orthographic projection) because that’s a pretty close starting point and added a bunch of control points.

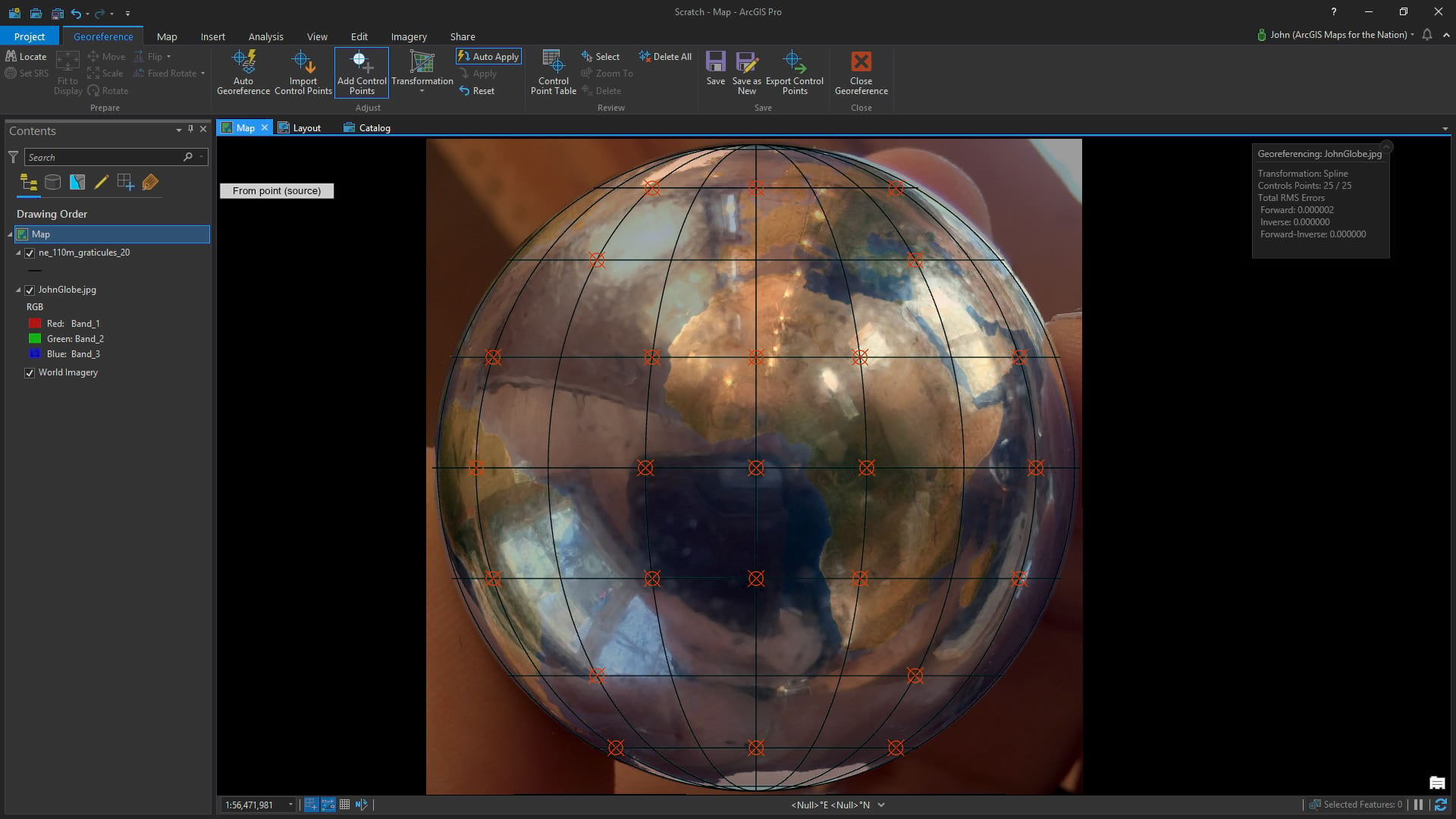
But an orthographic projection re-creates a sort of impossible view of earth because it puts our viewing perspective at an infinite distance, while my camera was only a couple inches away from this sphere. More on that later.

Re-Projecting

Once the sphere-portrait is georeferenced, I can easily re-project it to all sorts of cool views. Here is an example of the World From Space projection with a custom center-point (right click a projection, choose “copy and modify” then go to town). Because I’m now a geographically sentient overlay, the effect is me being rotated out of view.

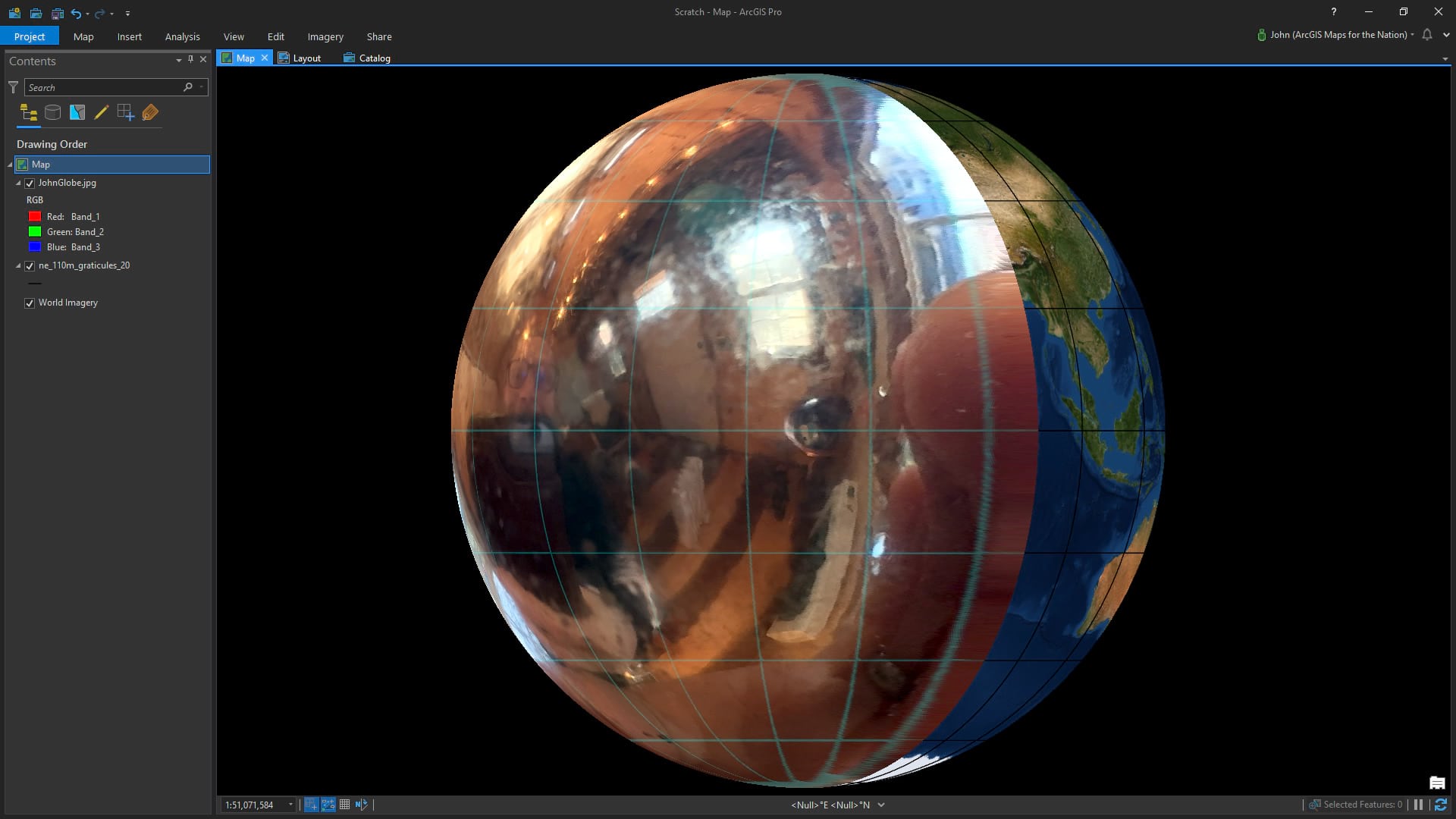
Here I am in Web Mercator…

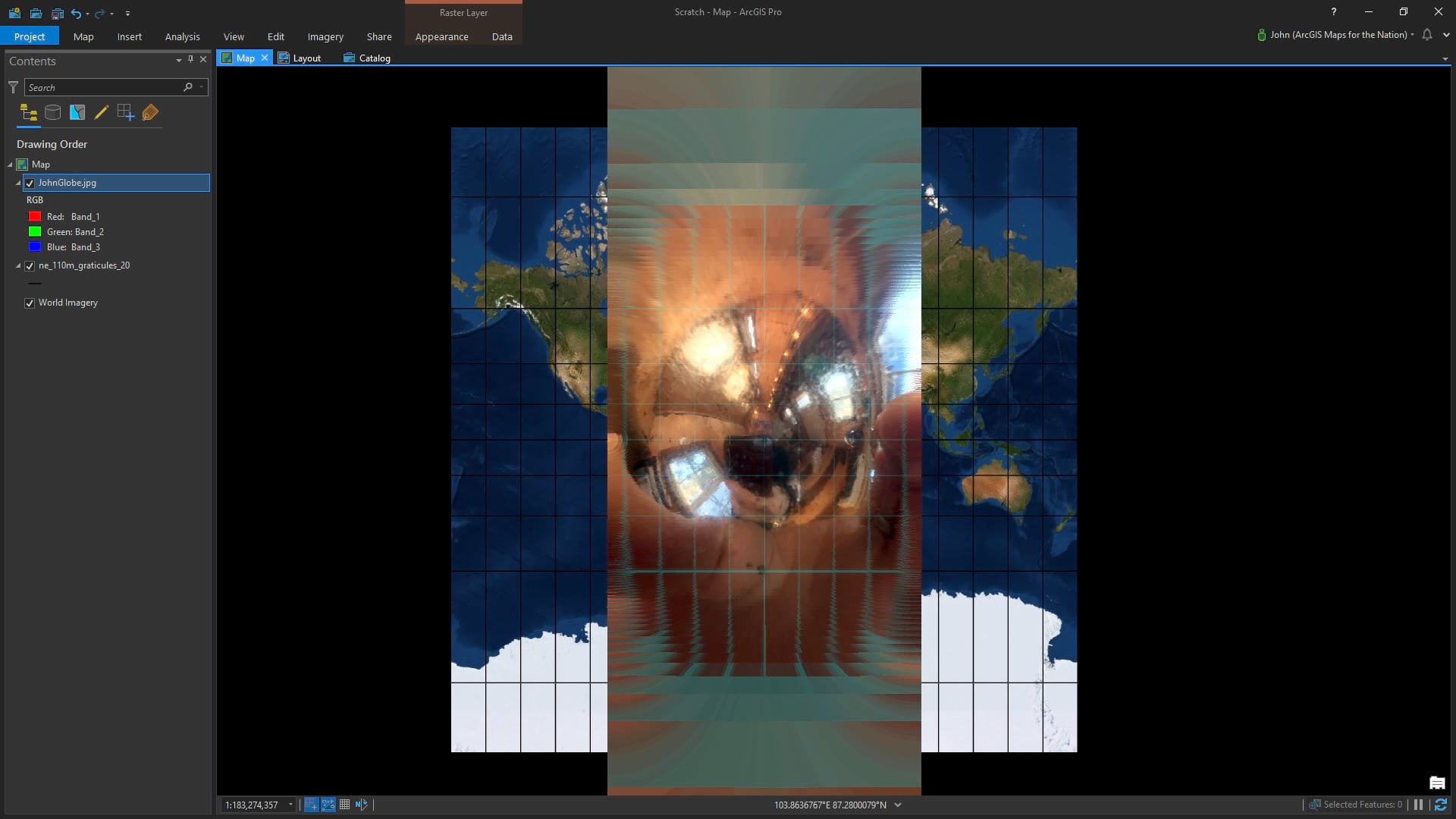
Distortions

Couple interesting things to note, here. First of all, the north and south poles of my metallic portrait push way off the map. This is because it’s the nature of Mercator to extend the poles into infinity. On web maps we just clip the world at like 85° (or something close, I don’t remember exactly). Infinity is hard.

Focal Length

The second interesting thing is that my metallic portrait only covers about half way around the world. Because I was starting with a photo of a sphere, my re-projected image can never cover more than half of the earth. In this case it’s worse than that because of focal length. When I hold my camera close to the sphere I’m seeing less of the surface. To see fully half of the sphere I’d need to hold my camera at an infinite distance.

Here’s what I mean…

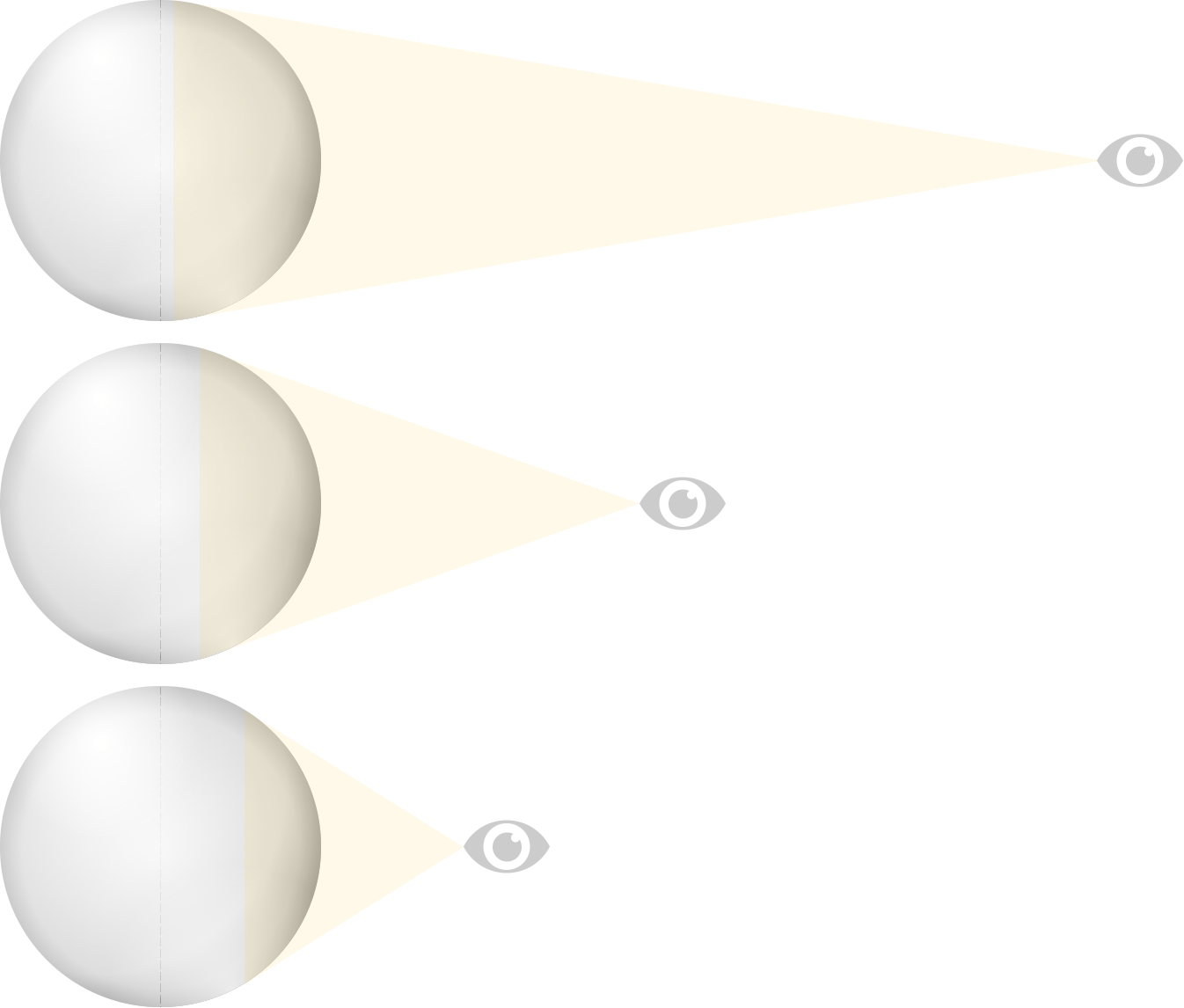
Remember that cool scene in The Fellowship of the Rings when Frodo looks down the road and it looks like it warps in a trippy way and he’s all “get off the road!”?

Here, re-live it for just a moment (also, this specific scene is almost a shot-for-shot re-do of the 1978 animated film)…

It’s a cool camera trick where they zoom the camera in while they physically move in camera backward. Or the other way around, I can’t work it out in my mind.

Registering satellite (but especially airphoto) imagery to the surface of the earth has to take this sort of perspective trapping into account, to replicate a camera that’s sitting at an infinite distance (orthographic) so everything’s rectified to its true geographic location without the misalignment of content due to perspective (or the earth’s surface falling away as you get further from dead-center). Orthorectification.

Un-globe-ing

Here’s a more literal example. This is a mass-produced globe ornament Danielle got me from Pier One Imports 20 years ago.

Here it is with a bunch of registration points using a spline transformation…

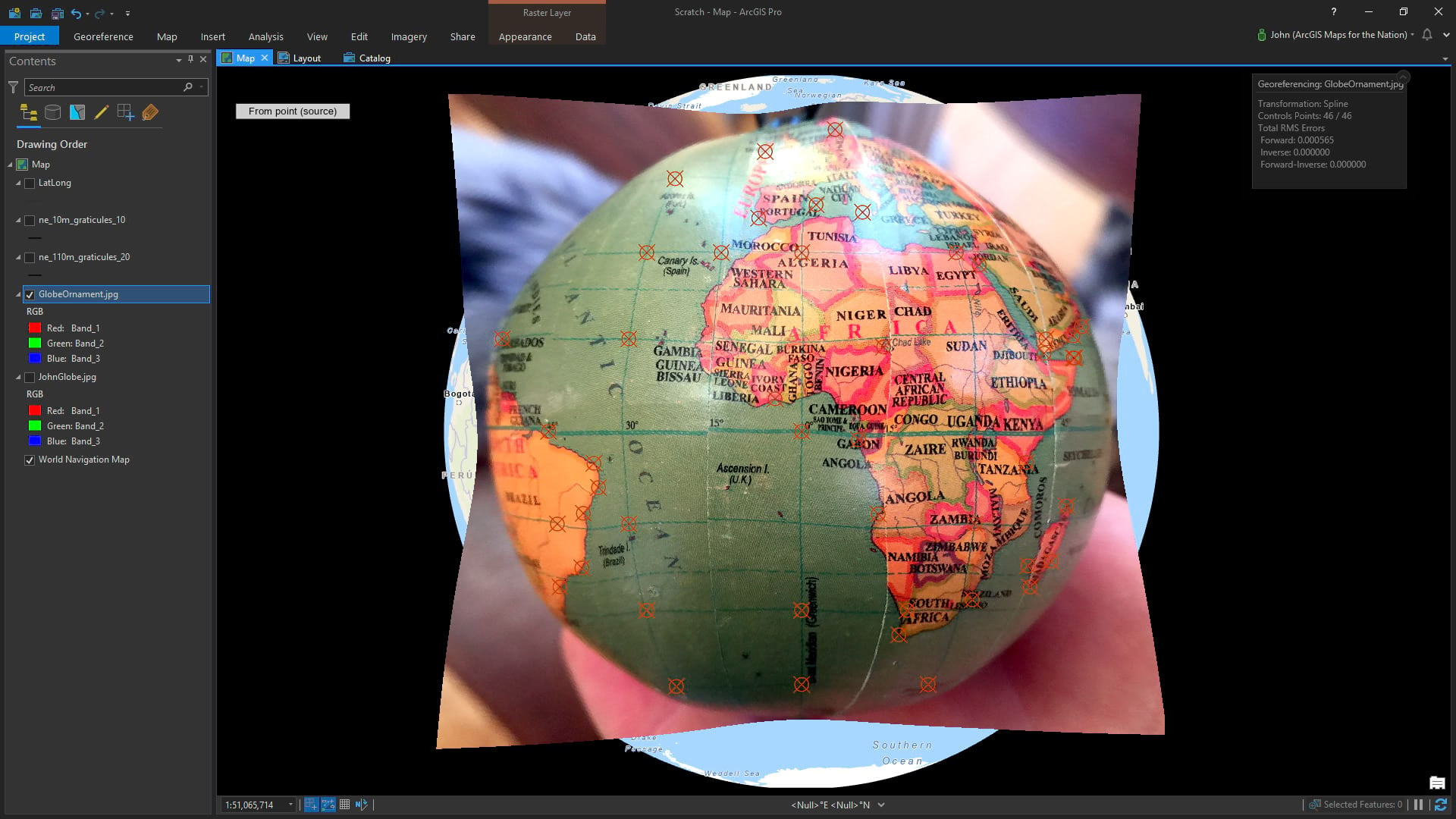
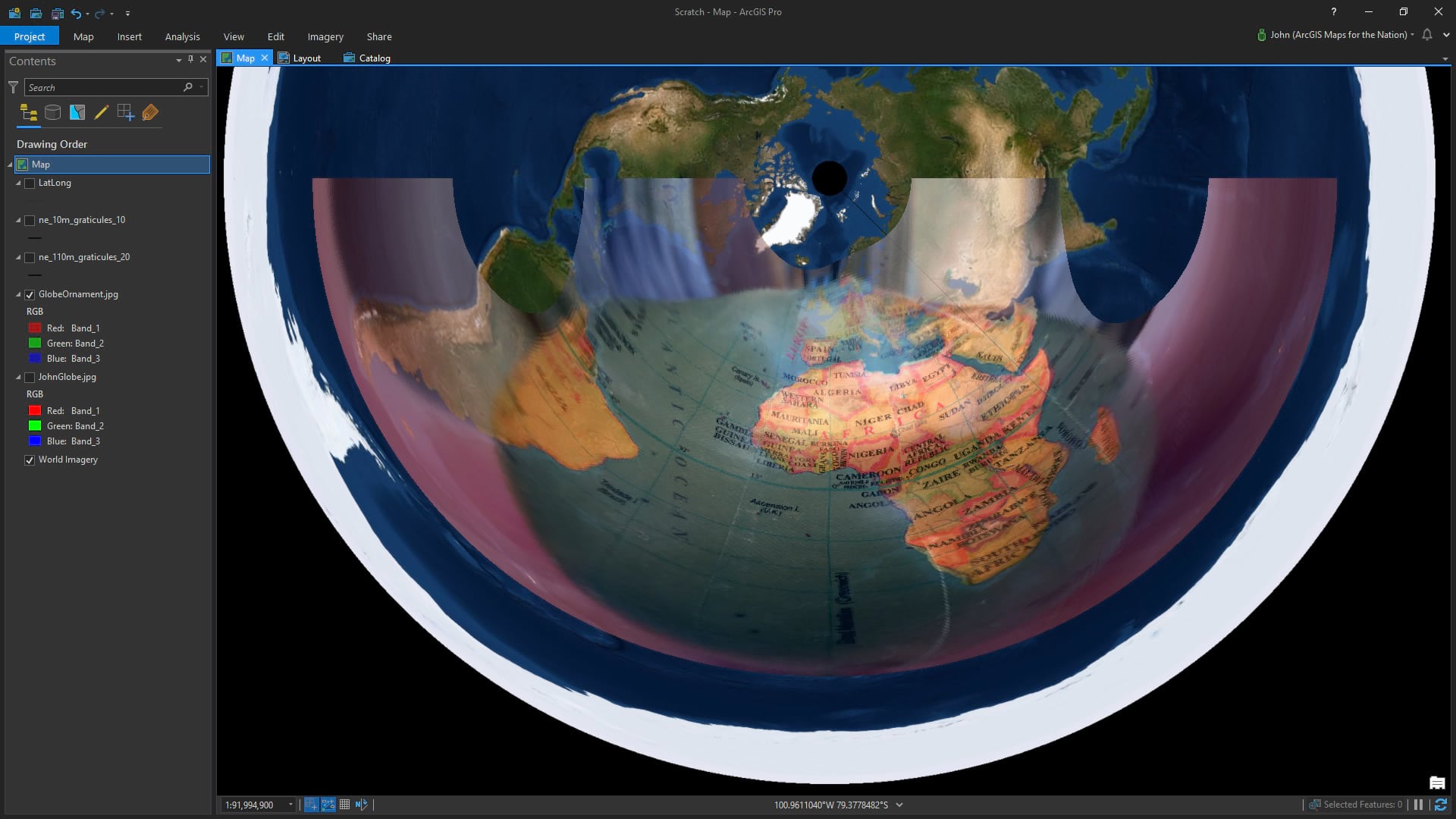
See how the globe doesn’t fully cover the orthographic basemap (which, by its nature, mathematically cheats to show an entire hemisphere)? That’s because my camera distance was a few inches so the area of coverage is much less than a hemisphere.

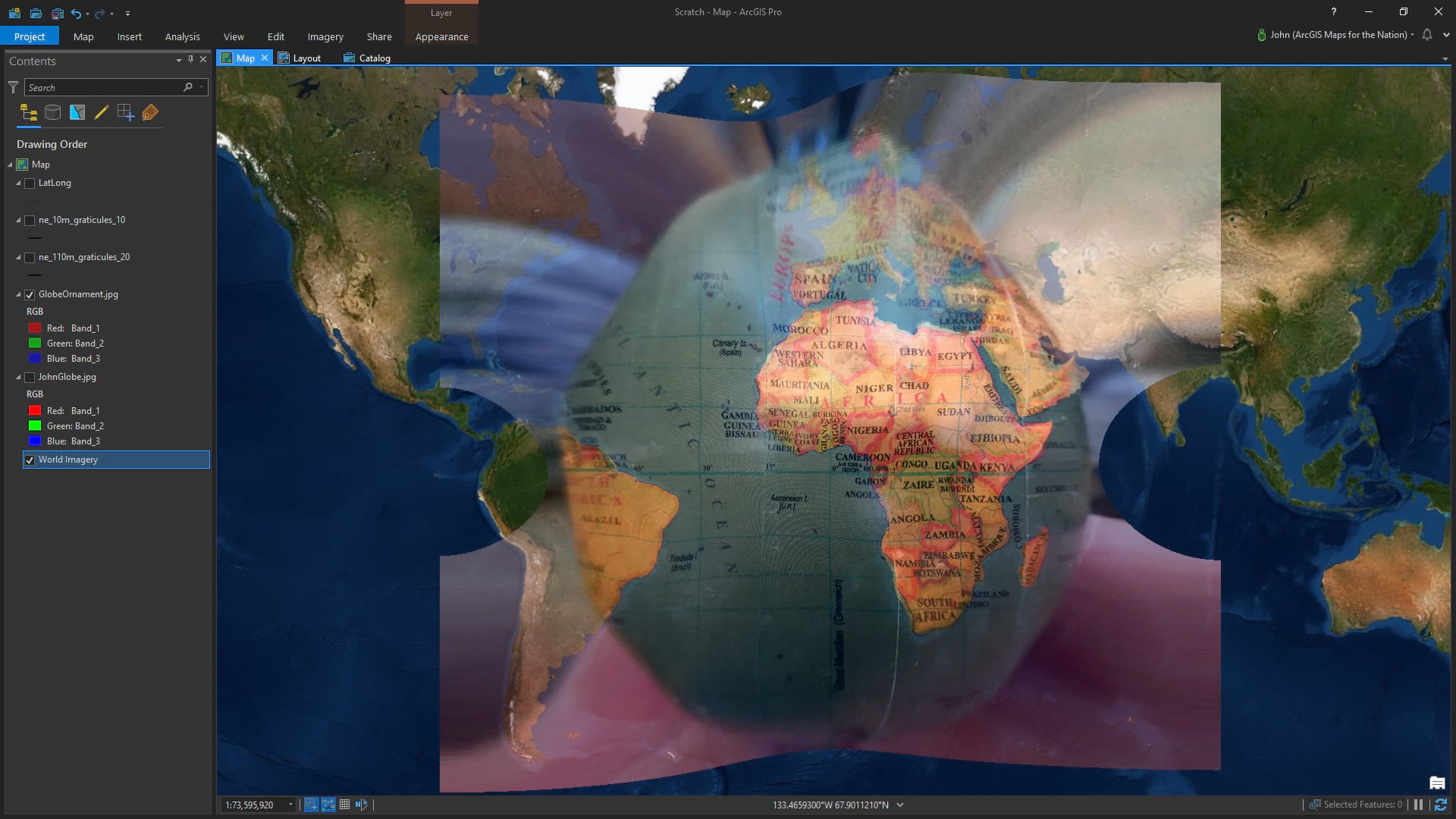
This becomes especially evident when the viewable area of the little globe is re-projected. Here it is in Web Mercator…

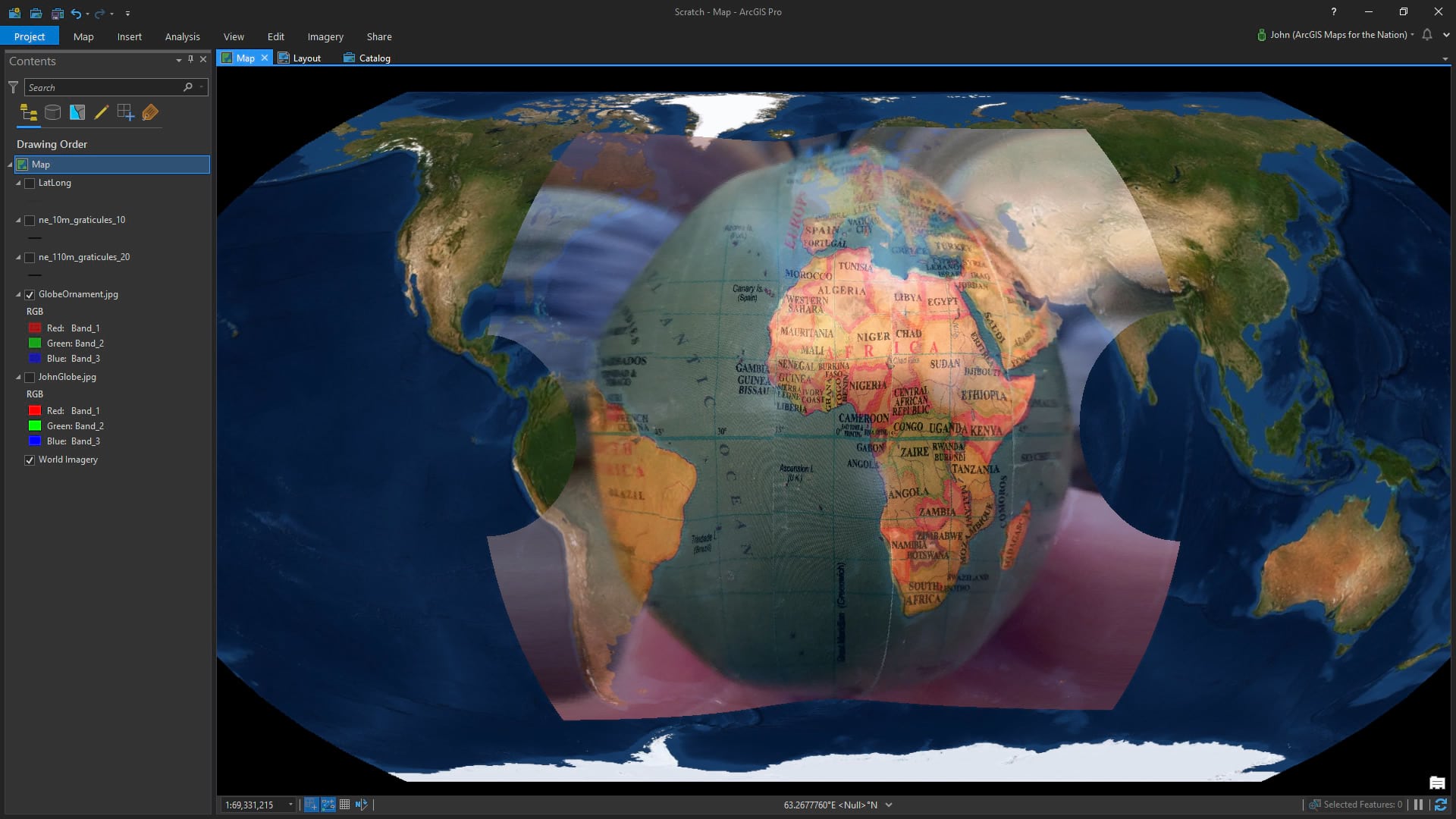
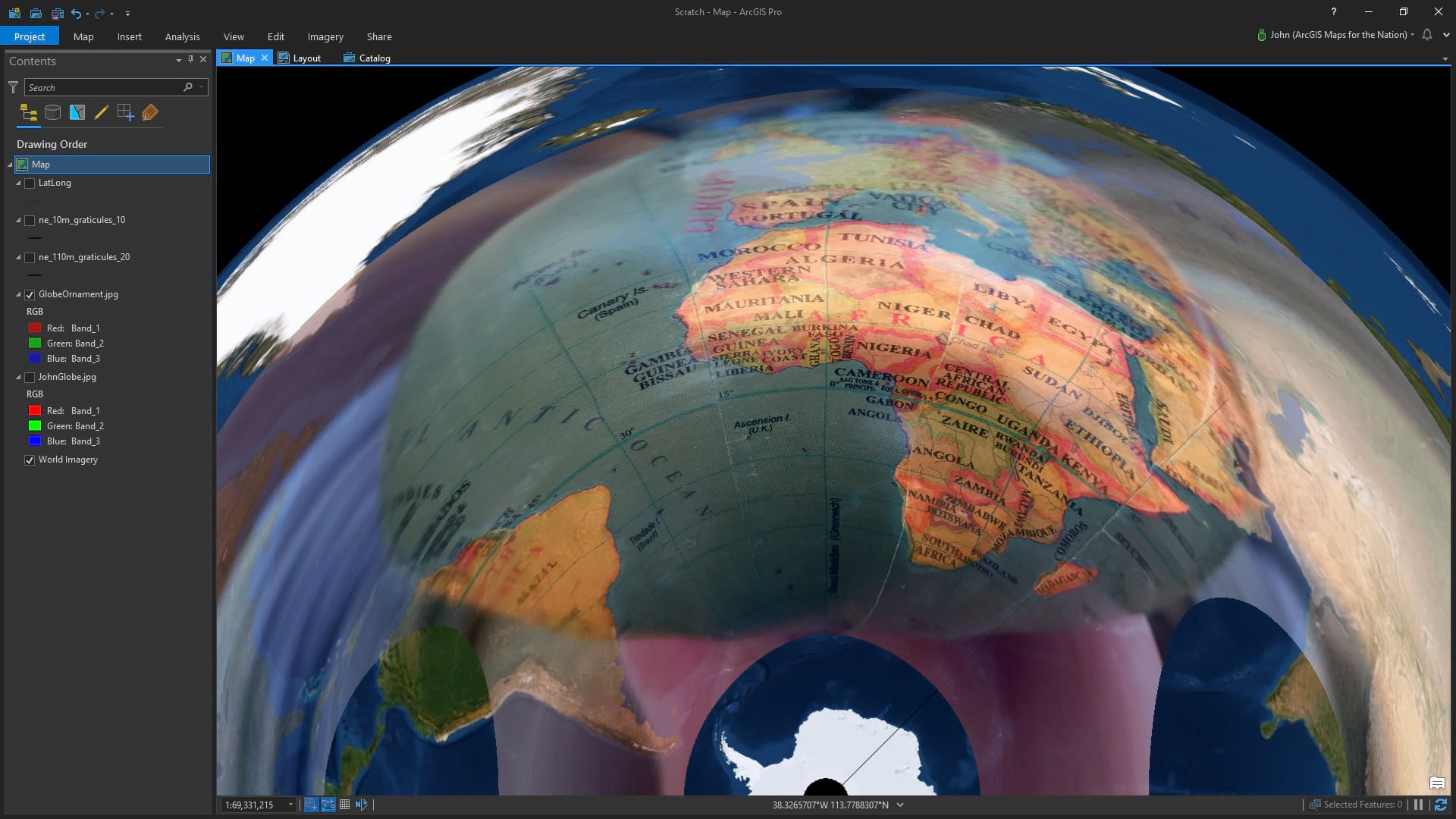
And here it is in the much more interesting and useful Equal Earth…

For kicks, here it is in both north and south pole versions of Azimuthal Equidistant…

If you are interested in seeing more examples of this, and all sorts of projection weirdnesses and examples, check out Cartography. Here is a page where Wesley Jones uses the familiar shape of an airplane to illustrate distortions.

Happy Projecting! John