Many datapoints have some level of uncertainty around them. Exhibit A for this is American Community Survey data from the United States Census Bureau. For this survey, the Census Bureau actually publishes margins of error, or ranges, around their estimates. For example, if the estimate for a certain group of people for an area is 361 people, there will be an associated margin of error for that estimate. If the margin of error is 158, the true number of people in that group there falls somewhere between 203 and 519.

Essentially, what we are trying to map are ranges. How can we map ranges?
If you map these ranges with traditional drawing styles such as graduated colors or graduated symbols using classification methods such as Natural Breaks or Quantile, you run into the problem of ranges spanning across two (or more) classes. In the example above, the estimate for a given feature is 361, but the range is 203 to 519. Typical classes such as 0 to 250, 251 to 500, and 500+ pose a problem.
The fundamental issue is that your map’s classes have hard edges and no differentiation within them, but your data has soft edges that by definition defy classification.
Unclassed symbology
With unclassed symbology, I no longer have to worry that a feature could be in more than one class. Unclassed symbology distributes your data into incrementally unique symbols. This results in a much more nuanced map, since the data is not constricted. Let’s take a look at two examples, one using color and one using size.
Classified vs. unclassed color
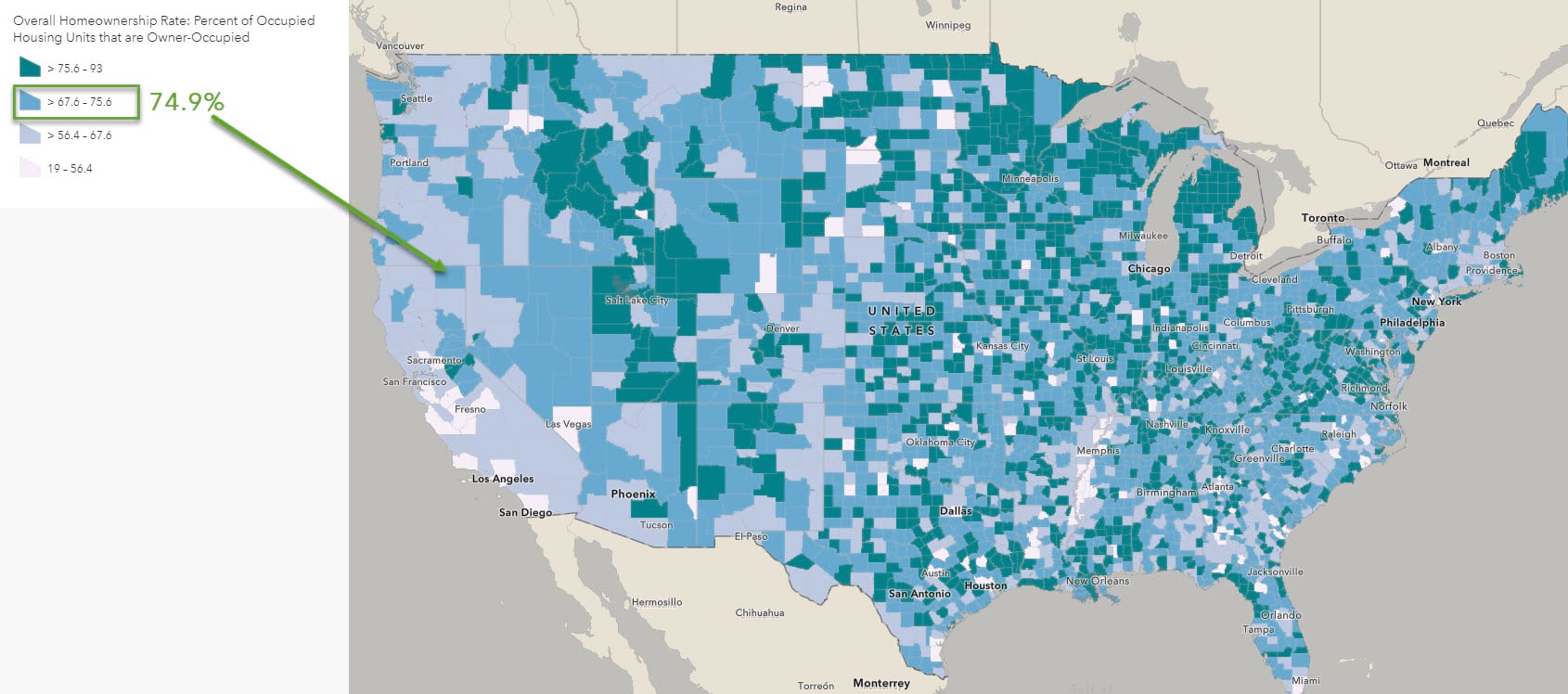
Here’s a map of homeownership rates. The estimate for Modoc County, CA is 74.9 percent, but the range is 74.2 to 77.5. Using the suggested default breaks using Natural Breaks, this puts Modoc County in two different classes.
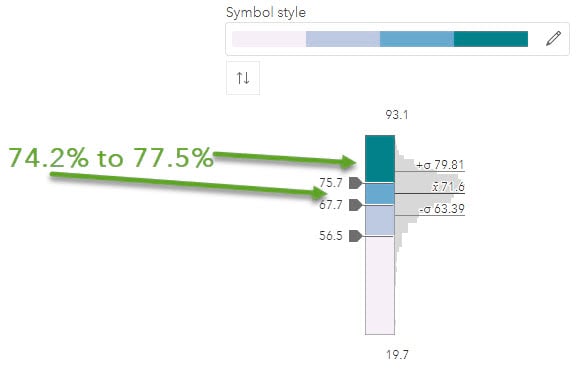
The resulting map shows Modoc County depicted by the second-darkest blue, based on the estimate of 74.9 percent. And yet, part of the range would warrant it being depicted by the darkest blue. How many other counties are likewise misrepresented on this map?
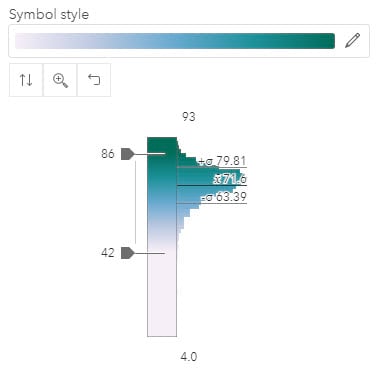
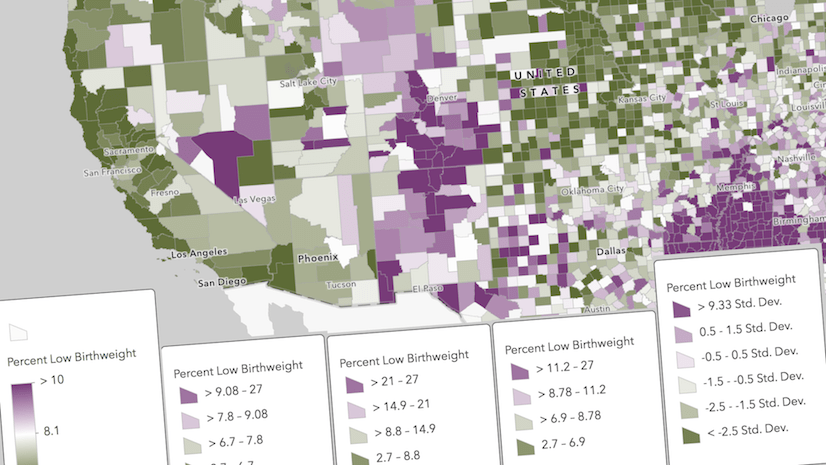
Unclassed color takes the darkest and lightest colors in a ramp, and incrementally distributes them across the distribution. The suggested default is one standard deviation above the mean and above get the darkest color, one standard deviation below the mean and below get the lightest color, and the majority of your data gets a unique color. As the map author, you can adjust these breakpoints for further fine-tuning. I did that here by extending the two breakpoints to cover more of the distribution.
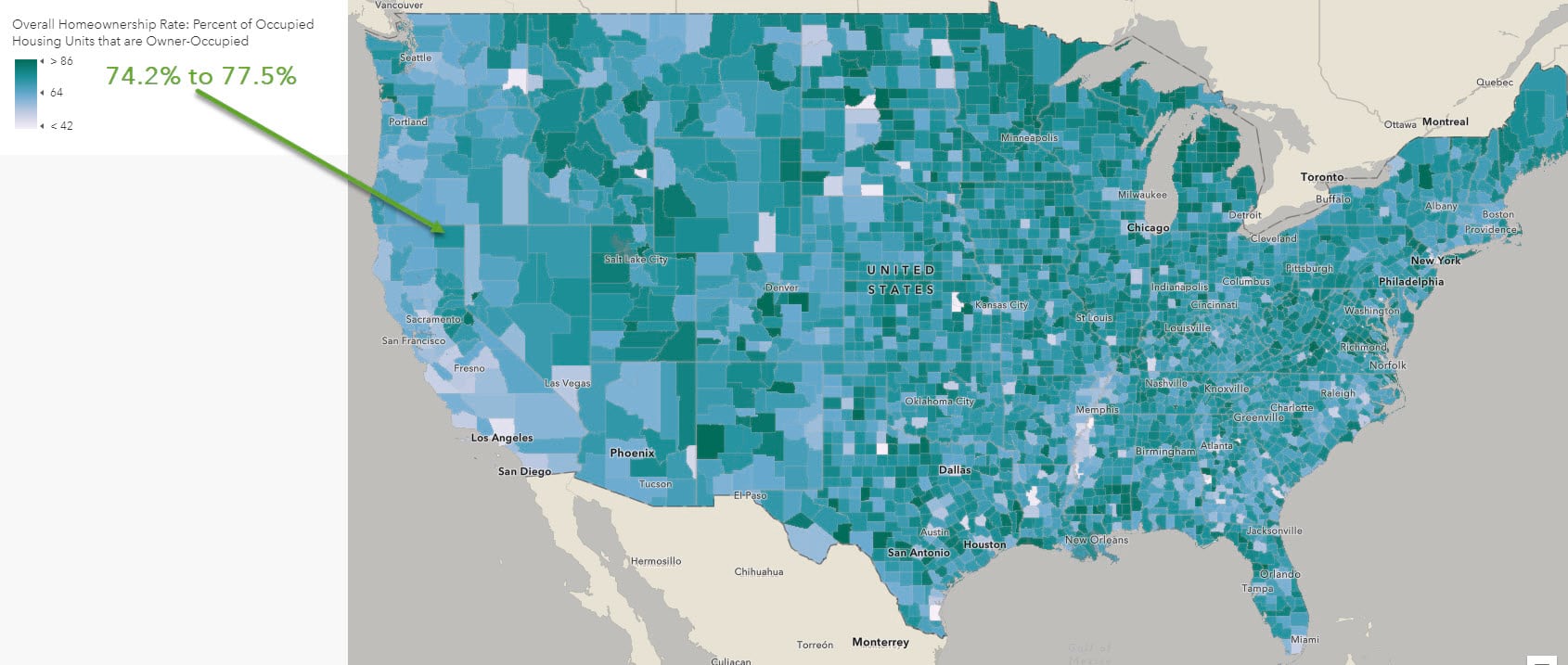
In the example below, ArcGIS Online Map Viewer varies the colors for values between 86 and 42. Each feature whose estimate is within that range gets a unique color. This minimizes the impact of uncertainty. The darkest color in the color ramp is shared by all values greater than 86, and the lightest color in the color ramp is shared by all values lower than 42.
The range of data will get an appropriate color. Recall that the homeownership rate for Modoc County, CA is 74.9 percent, but the range is 74.2 to 77.5. Another hypothetical county whose rate is closer to 67.8 (right above the breakpoint between the second and third class above) will get a lighter color, whereas in the classified map above, it would receive the same color. A lighter color is appropriate since it’s a lower value, and additionally, there’s no concern that the range of this other county would span the second and third class. If its range overlaps with Modoc County’s range, that’s okay. The unclassed map honors these ranges much better:
Classified vs. unclassed size
While color is best for mapping percents or rates, size is best for mapping counts or amounts. Let’s use vacant housing units as our count attribute, an attribute notorious for very large margins of error, or very large ranges.
Notice a classified version (using Natural Breaks) has only a few different sizes of symbols. Variation within the classes is not displayed. There’s also the same potential for a range to span two or more classes.
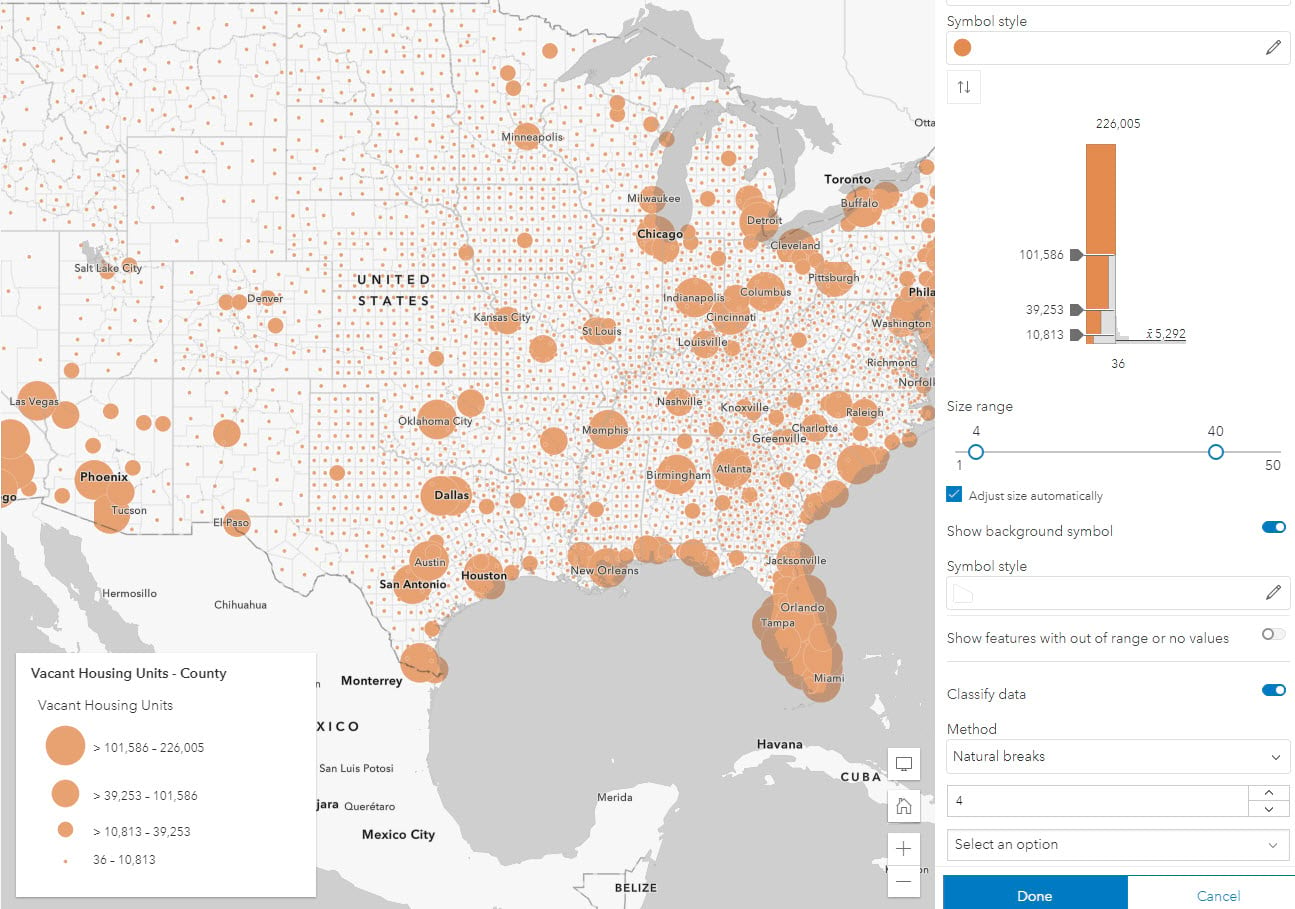
An unclassed version has many differently-sized symbols. Notice the counties here in Florida and the Gulf Coast, where lots of variation is displayed by the size:
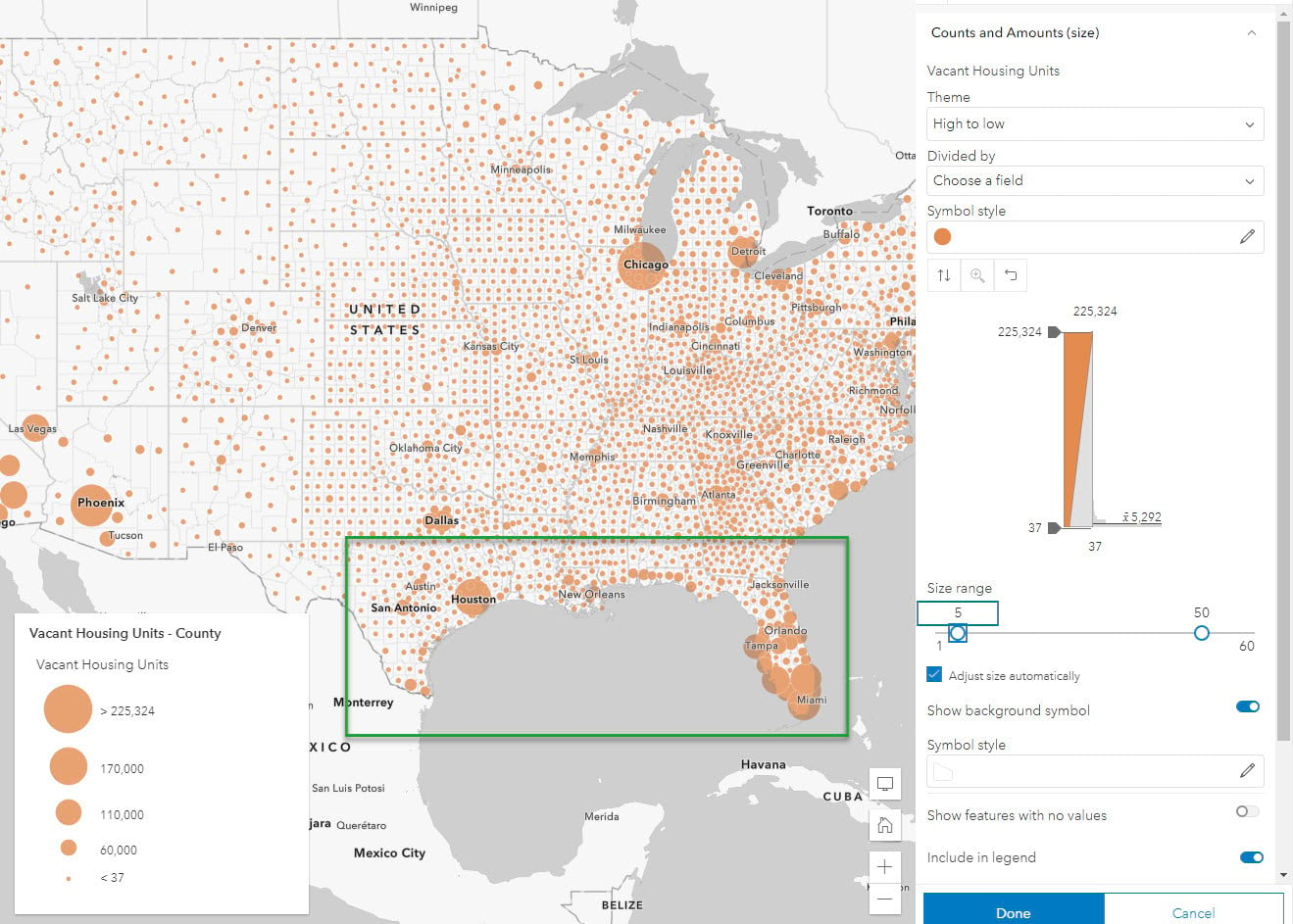
The problem of a range spanning multiple classes is diminished, as unclassed size ramps allow the data to breathe.
Final Thoughts
When mapping ranges (and, if you’re mapping American Community Survey data, you are!), unclassed symbology eliminates the concern that a feature could potentially be in more than one class. This is true for both unclassed color and unclassed size. An additional benefit is that you get a more nuanced map. You may have noticed that the American Community Survey layers in ArcGIS Living Atlas use unclassed symbology. If you’re interested in mapping the actual margins of error, we have some ideas for you in this ArcGIS Learn Path.
Thoughts on symbolizing overlapping ranges? Head over to Esri Community’s Cartography and Maps space where you’ll find a community of mappers and cartographers exchanging ideas.


Article Discussion: