 Late last year I introduced ArcGIS users to sports analytics, an emerging and exciting field within the GIS industry. Using ArcGIS for sports analytics can be read here. Recently I expanded the work by using a number of spatial analysis tools in ArcGIS to study the spatial variation of serve patterns from the London Olympics Gold Medal match played between Roger Federer and Andy Murray. In this blog I present results that suggest there is potential to better understand players serve tendencies using spatio-temporal analysis.
Late last year I introduced ArcGIS users to sports analytics, an emerging and exciting field within the GIS industry. Using ArcGIS for sports analytics can be read here. Recently I expanded the work by using a number of spatial analysis tools in ArcGIS to study the spatial variation of serve patterns from the London Olympics Gold Medal match played between Roger Federer and Andy Murray. In this blog I present results that suggest there is potential to better understand players serve tendencies using spatio-temporal analysis.
 Figure 1: Igniting further exploration using visual analytics. Created in ArcScene, this 3D visualization depicts the effectiveness of Murray’s return in each rally and what effect it had on Federer’s second shot after his serve. (click to enlarge)
Figure 1: Igniting further exploration using visual analytics. Created in ArcScene, this 3D visualization depicts the effectiveness of Murray’s return in each rally and what effect it had on Federer’s second shot after his serve. (click to enlarge)
The Most Important Shot in Tennis?
The serve is arguably the most important shot in tennis. The location and predictability of a players serve has a big influence on their overall winning serve percentage. A player is who is unpredictable with their serve, and can consistently place their serve wide into the service box, at the body or down the T is more likely to either win a point outright, or at least weaken their opponent’s return [1].
The results of tennis matches are often determined by a small number of important points during the game. It is common to see a player win a match who has won the same number of points as his opponent. The scoring system in tennis also makes it possible for a player to win fewer points than his opponent yet win the match [2]. Winning these big points is critical to a player’s success. For the player serving, their aim is to produce an ace or, force their opponent into an outright error, as this could make the difference between winning and losing. It is of particular interest to coaches and players to know the success of players serve at these big points.
Geospatial Analysis
In order to demonstrate the effectiveness of geo-visualizing spatio-temporal data using GIS we conducted a case study to determine the following: Which player served with more spatio-temporal variation at important points during the match?
To find out where each player served during the match we plotted the x,y coordinate of the serve bounce. A total of 86 points were mapped for Murray, and 78 for Federer. Only serves that landed in were included in the analysis. Visually we could see clusters formed by wide serves, serves into the body and serves hit down the T. The K Means algorithm [3] in the Grouping Analysis tool in ArcGIS (Figure 2) enabled us to statically replicate the characteristics of the visual clusters. It enabled us to tag each point as either a wide serve, serve into the body or serve down the T. The organisation of the serves into each group was based on the direction of serve. Using the serve direction allowed us to know which service box the points belong to. Direction gave us an advantage over proximity as this would have grouped points in neighbouring service boxes.
Figure 2. The K Means algorithm in the Grouping Analysis tool in ArcGIS groups features based on attributes and optional spatial temporal constraints.
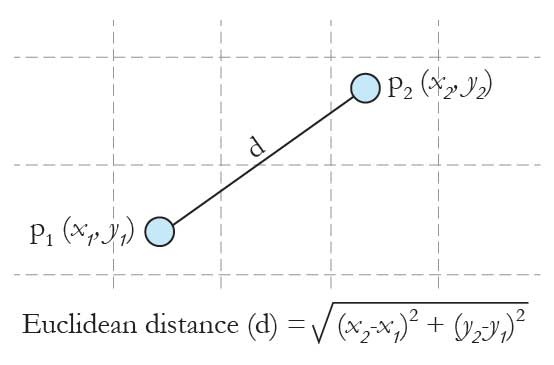
To determine who changed the location of their serve the most we arranged the serve bounces into a temporal sequence by ranking the data according to the side of the net (left or right), by court location (deuce or ad court), game number and point number. The sequence of bounces then allowed us to create Euclidean lines (Figure 3) between p1 (x1,y1) and p2 (x2,y2), p2 (x2,y2) and p3 (x3,y3), p3 (x3,y3) and p4 (x4,y4) etc in each court location. It is possible to determine, with greater spatial variation, who was the more predictable server using the mean Euclidean distance between each serve location. For example, a player who served to the same part of the court each time would exhibit a smaller mean Euclidean distance than a player who frequently changed the position of their serve. The mean Euclidean distance was calculated by summing all of the distances linking the sequence of serves in each service box divided by the total number of distances.
Figure 3. Calculating the Euclidean distance (shortest path) between two sequential serve locations to identify spatial variation within a player’s serve pattern.
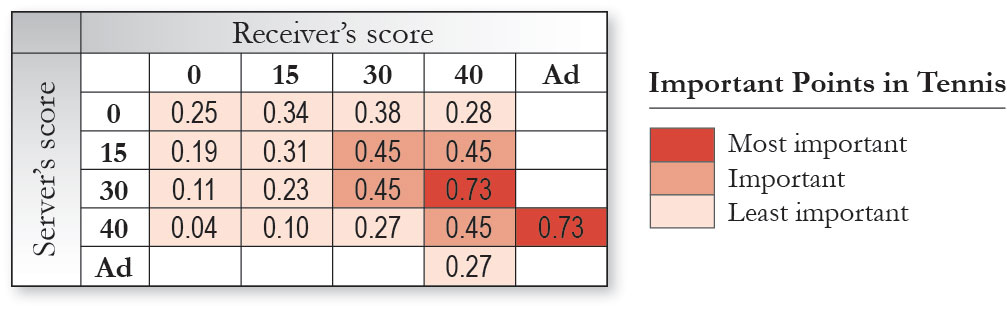
To identify where a player served at key points in the match we assigned an importance value to each point based on the work by Morris [4]. The table in Figure 4 shows the importance of points to winning a game, when a server has 0.62 probability of winning a point on serve. This shows the two most important points in tennis are 30-40 and 40-Ad, highlighted in dark red. To simplify the rankings we grouped the data into three classes, as shown in Figure 4.
Figure 4. The importance of points in a tennis match as defined by Morris. The data for the match was classified into 3 categories as indicated by the sequential colour scheme in the table (dark red, medium red and light red).
In order see a relationship between outright success on a serve at the important points we mapped the distribution of successful serves and overlaid the results onto a layer containing the important points. If the player returning the serve made an error directly on their return, then this was deemed to be an outright success for the player. An ace was also deemed to be an outright success for the server.
Results
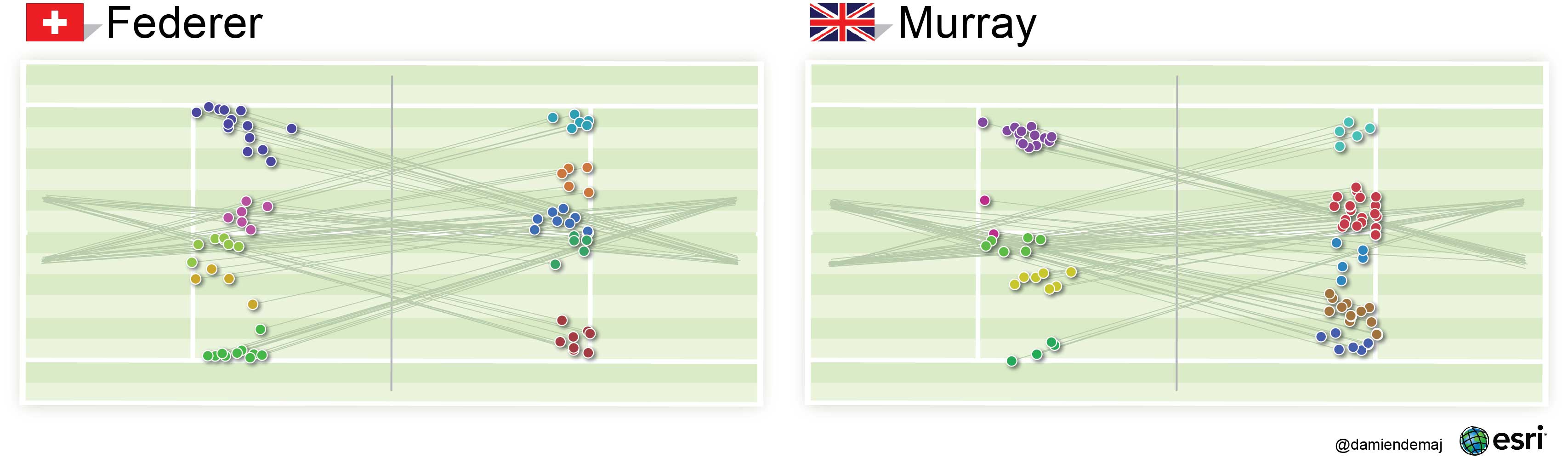
Federer’s spatial serve cluster in the ad court on the left side of the net was the most spread of all his clusters. However, he served out wide with great accuracy into the deuce court on the left side of the net by hugging the line 9 times out 10 (Figure 5). Murray’s clusters appeared to be grouped overall more tightly in each of the service boxes. He showed a clear bias by serving down the T in the deuce court on the right side of the net. Visually there appeared to be no other significant differences between each player’s patterns of serve.
Figure 5. Mapping the spatial serve clusters using the K Means Algorithm. Serves are grouped according to the direction they were hit. The direction of each serve is indicated by the thin green trajectory lines. The direction of serve was used to statistically group similar serve locations. (click to enlarge)
By mapping the location of the players serve bounces and grouping them into spatial serve clusters we were able to quickly identify where in the service box each player was hitting their serves. The spatial serve clusters, wide, body or T were symbolized using a unique color, making it easier for the user to identify each group on the map. To give the location of each serve some context we added the trajectory (direction) lines for each serve. These lines helped link where the serve was hit from to where the serve landed. They help enhance the visual structure of each cluster and improve the visual summary of the serve patterns.
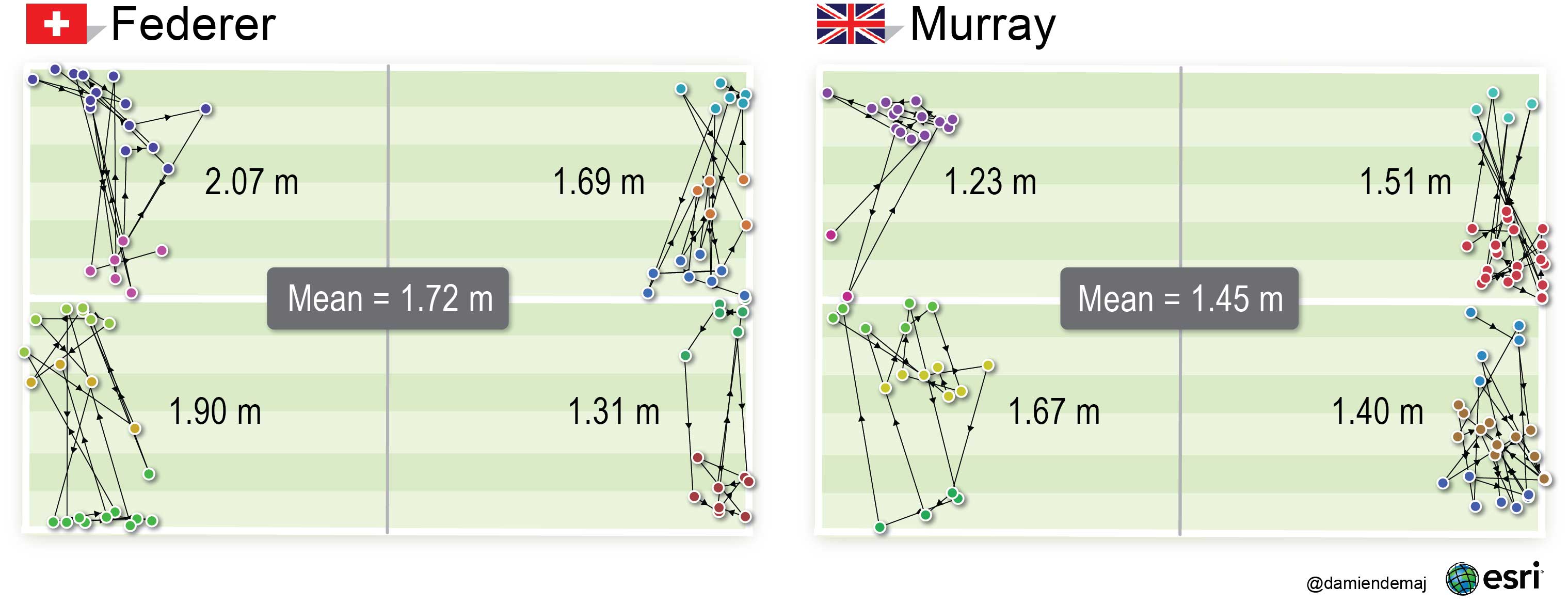
The Euclidean distance calculations showed Federer’s mean distance between sequential serve bounces was 1.72 m (5.64 ft), whereas Murray’s mean Euclidean distance was 1.45 m (4.76 ft). These results suggest that Federer’s serve had greater spatial variation than Murray’s. Visually, we could detect that the network of Federer’s Euclidean lines showed a greater spread than Murray’s in each service box. Murray served with more variation than Federer in only one service box, the ad service box on the right side of the net.
Figure 6. A comparison of spatial serve variation between each player. Federer’s mean Euclidean distance was 1.72m (5.64 ft) – Murrray’s was 1.45m (4.76 ft). The results suggest that Federer’s serve had greater spatial variation than Murray’s. The lines of connectivity represent the Euclidean distance (shortest path) between each sequential service bounce in each service box. (click to enlarge)
The directional arrows in Figure 6 allow us to visually follow the temporal sequence of serves from each player in any given service box. We have maintained the colors for each spatial serve cluster (wide, body, T) so you can see when a player served from one group into another.
At the most important points in each game (30-40 and 40-Ad), Murray served out wide targeting Federer’s backhand 7 times out of 8 (88%). He had success doing this 38% of the time, drawing 3 outright errors from Federer. Federer mixed up the location of his 4 serves at the big points across all of the spatial serve clusters, 2 wide, 1 body and 1 T. He had success 25% of the time drawing 1 outright error from Murray. At other less important points Murray tended to favour going down the T, while Federer continued his trend spreading his serve evenly across all spatial serve clusters (Figure 7).
The proportional symbols in Figure 7 indicate a level of importance for each serve. The larger circles represent the most important points in each game – the smallest circles the least important. The ticks represent the success of each serve. By overlaying the ticks on-top of the graduated circles we can clearly see a relationship between the success at big points on serve. The map also indicates where each player served.
Figure 7. A proportional symbol map showing the relationship of where each player served at big points during the match, and their outright success at those points. (click to enlarge)
The results suggest that Murray served with more spatial variation across the two most important point categories, recording a mean Euclidean distance of 1.73 m (5.68 ft) to Federer’s 1.64 m (5.38 ft).
Conclusion
Successfully identifying patterns of behavior in sport in an on-going area of work [5] (see figure 8), be that in tennis, football or basketball. The examples in this blog show that GIS can provide an effective means to geovisualize spatio-temporal sports data, in order to reveal potential new patterns within a tennis match. By incorporating space-time into our analysis we were able to focus on relationships between events in the match, not the individual events themselves. The results of our analysis were presented using maps. These visualizations function as a convenient and comprehensive way to display the results, as well as acting as an inventory for the spatio-temporal component of the match [6].
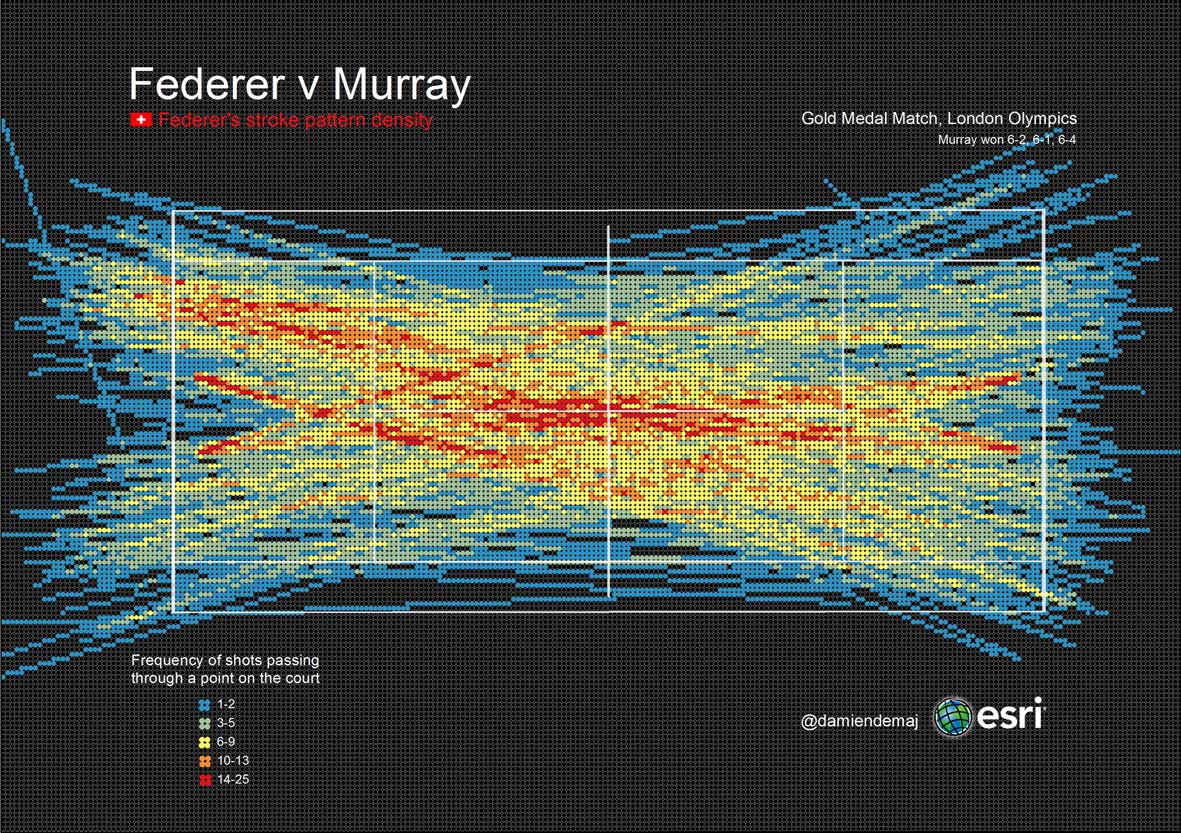
Figure 8. The heatmap above shows Federer’s frequency of shots passing through a given point on the court. The map displays stroke paths from both ends of the court, including serves. The heat map can be used to study potential anomalies in the data that may result in further analysis. (click to enlarge)
Expanding the scope of geospatial research in tennis, and other sports relies on open access to reliable spatial data. At present, such data is not publically available from the governing bodies of tennis. An integrated approach with these organizations, players, coaches, and sports scientists would allow for further validation and development of geospatial analytics for tennis. The aim of this research is to evoke a new wave of geospatial analytics in the game of tennis and across other sports. Furthermore, to encourage statistics published on tennis to become more time and space aware to better improve the understanding of the game, for everyone.
The full research paper, and an in depth discussion about the importance of understanding space-time relationships in sport can be read here.
Damien is Geospatial Product Engineer at Esri. @damiendemaj
References
[1] United States Tennis Association, “Tennis tactics, winning patterns of play”, Human Kinetics, 1st Edition, 1996.
[2] G. E. Parker, “Percentage Play in Tennis”, In Mathematics and Sports Theme Articles, http://www.mathaware.org/mam/2010/essays/
[3] J. A. Hartigan and M. A. Wong, “Algorithm AS 136: A K-Means Clustering Algorithm”, Journal of the Royal Statistical Society. Series C (Applied Statistics), vol. 28, No. 1, pp. 100-108, 1979.
[4] C. Morris, “The most important points in tennis”, In Optimal Strategies in Sports, vol 5 in Studies and Management Science and Systems, , North-Holland Publishing, Amsterdam, pp. 131-140, 1977.
[5] M. Lames, “Modeling the interaction in games sports – relative phase and moving correlations”, Journal of Sports Science and Medicine, vol 5, pp. 556-560, 2006.
[6] J. Bertin, “Semiology of Graphics: Diagrams, Networks, Maps”, Esri Press, 2nd Edition, 2010.

Commenting is not enabled for this article.